トップ > Codeforces > Codeforces Round #337 (Div. 2)

Codeforces Round #337 (Div. 2)

Codeforces

Codeforcesは2回目の参加。

A. Pasha and Stick

問題概要

Pasha has a wooden stick of some positive integer length n. He wants to perform exactly three cuts to get four parts of the stick. Each part must have some positive integer length and the sum of these lengths will obviously be n.

Pasha likes rectangles but hates squares, so he wonders, how many ways are there to split a stick into four parts so that it's possible to form a rectangle using these parts, but is impossible to form a square.

Your task is to help Pasha and count the number of such ways. Two ways to cut the stick are considered distinct if there exists some integer x, such that the number of parts of length x in the first way differ from the number of parts of length x in the second way.
簡単な意訳
長さnの木の棒があります。4本に切って長方形（正方形ではない）を作るとき、出来る長方形は何通りありえるでしょう。

解法

（問題文に偶数と指定があるかもしれませんが）まずnが奇数の時は長方形が出来ません。答えは0。
nが偶数の時、長方形の周になるので取り敢えず1/2にしましょう。n/2が偶数ならn/4-1(正方形になる分）、奇数ならn/4です。

#include <bits/stdc++.h>
using namespace std;
int main(){
	int n;	cin>>n;
	if(n%2==1)	cout<<0<<endl;
	else{
		n/=2;
		if(n%2==1)	cout<<(int)n/2<<endl;
		else 	cout<<n/2-1<<endl;
	}
	return 0;
}

B. Vika and Squares

問題概要

Vika has n jars with paints of distinct colors. All the jars are numbered from 1 to n and the i-th jar contains ai liters of paint of color i.

Vika also has an infinitely long rectangular piece of paper of width 1, consisting of squares of size 1 × 1. Squares are numbered 1, 2, 3 and so on. Vika decided that she will start painting squares one by one from left to right, starting from the square number 1 and some arbitrary color. If the square was painted in color x, then the next square will be painted in color x + 1. In case of x = n, next square is painted in color 1. If there is no more paint of the color Vika wants to use now, then she stops.

Square is always painted in only one color, and it takes exactly 1 liter of paint. Your task is to calculate the maximum number of squares that might be painted, if Vika chooses right color to paint the first square.
簡単な意訳
n個の瓶があり、それぞれaiリットルのペンキが入っている。瓶に入っているペンキの色は全て別の色で、ある番号から(その番号+1)、(+2)、…と1リットルずつ使っていく。番号がNになったら次は1としてどんどん塗っていき、塗りたいペンキの中身が0になっていたら終了。最善の選び方をしたとき、何リットル塗ることができるか求めよ。

解法

どこから塗り始めたかに関わらず、取り敢えず全体の瓶の中で1番中身の少ない瓶が尽きて、そこで止まる。ということで(一番中身の少ない瓶の中身)×(瓶の数)は絶対に使います。その分は引いてあげましょう。そうしたら、
cnt[i]=1(瓶iがまだ残っている),0(残っていない)
と定義し、「1が最大いくつ連続しているか」という問題に持ち込めます。N→1の間がそのままだと面倒なので、後ろにそのまま同じ配列をくっつけて対策。
cnt[i-1]>0ならcnt[i]=cnt[i-1]+1、そうでないならcnt[i]はそのまま、というように更新。全体の中での最大値を足して答えになります。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
	ll n;	cin>>n;
	vector<ll> a(n);
	ll sml=0;
	for(int i=0;i<n;i++){
		cin>>a[i];
		if(a[i]<a[sml])	sml=i;
	}
	ll rm=a[sml];
	ll ans=rm*n;
	for(int i=0;i<n;i++)	a[i]-=rm;
	a.insert(a.end(),a.begin(),a.end());
	n*=2;
	vector<ll> cnt(n);
	for(int i=0;i<n;i++)	cnt[i]=0;
	if(a[0]>0)	cnt[0]=1;
	ll ans2=0;
	for(int i=1;i<n;i++){
		if(a[i]>0)	cnt[i]=cnt[i-1]+1;
		ans2=max(ans2,cnt[i]);
	}
	cout<<ans+ans2<<endl;
	return 0;
}

C. Harmony Analysis

問題概要

The semester is already ending, so Danil made an effort and decided to visit a lesson on harmony analysis to know how does the professor look like, at least. Danil was very bored on this lesson until the teacher gave the group a simple task: find 4 vectors in 4-dimensional space, such that every coordinate of every vector is 1 or  - 1 and any two vectors are orthogonal. Just as a reminder, two vectors in n-dimensional space are considered to be orthogonal if and only if their scalar product is equal to zero, that is:
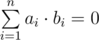
http://codeforces.com/predownloaded/54/c0/54c00469bf0b7938e8dae7c67efac5401de9ae35.png
Danil quickly managed to come up with the solution for this problem and the teacher noticed that the problem can be solved in a more general case for 2k vectors in 2k-dimensinoal space. When Danil came home, he quickly came up with the solution for this problem. Can you cope with it?
簡単な意訳
入力にkが与えられます。2^k次元のベクトルで、どの2つのベクトルの内積も0になるベクトルを2^k個列挙してください。
ただし、全要素は1と-1で構成されるようにしてください。

解法

取り敢えず、ベクトルという発想から抜けましょう。2^kの長さの0と1のビット列を考えます。ベクトルの時、(積が-1の数)==(積が1の数)なので、2つのビット列のXORの数が2^(k-1)個あればいいことになります。
この後は正直分からないので適当にk=3を考えました。(実は少しk=4もやっています)
答えはk=2の時
0000
0011
0101
0110
k=3の時には
00000000
00001111
00110011
00111100
01010101
01011010
01100110
01101001
となります。自分が気づいたのは、
「左半分だけ考えて、右側は左側と同じもの、+と*を入れ替えたものの2通り(2行ごとに区切ると分かる)」
ということです。これ、しかもk=3の左側のみで考えて、それをさらに半分に区切っても成立します。

この考察から、1文字目は+、以降今持っている文字列をそのまま後ろに繋げたものと+と*を入れ替えたものを繋げたものをさらに奥へ送ってあげる、という再帰関数を作ってあげればOKです。分割統治法、ですかね…（分かりません）

#include <bits/stdc++.h>
using namespace std;
void dfs(int k,string s){
	if(k==0){
		cout<<s<<endl;
		return;
	}
	string t="";
	for(int i=0;i<(int)s.size();i++){
		if(s[i]=='+')	t+='*';
		else 	t+='+';
	}
	dfs(k-1,s+s);	dfs(k-1,s+t);
}

int main(){
	int k;	cin>>k;
	dfs(k,"+");
}

結構この考察に時間取られました。でも思いついた時「これだ！！」と爽快感。だから競プロは止められない。


D. Vika and Segments

問題概要

Vika has an infinite sheet of squared paper. Initially all squares are white. She introduced a two-dimensional coordinate system on this sheet and drew n black horizontal and vertical segments parallel to the coordinate axes. All segments have width equal to 1 square, that means every segment occupy some set of neighbouring squares situated in one row or one column.

Your task is to calculate the number of painted cells. If a cell was painted more than once, it should be calculated exactly once.
簡単な意訳
グリッド上のマス目をn本の直線が通ります。何マス直線が通っていますか？

解法（解けてない）

これは見た瞬間「平面走査」だと分かりました。ググれば簡単に殆ど同じ問題があるので説明は省略します。
y座標毎にソートして、下から見ていけばいいのですが、平面走査はアルゴリズムは知っていながら実装したことがありませんでした。
考えながらなんとなくで実装して、1発でサンプル通ったし残り3分なので提出→WA→死亡の流れでした。
ちゃんと読んでおけば良かったな…（この本で見かけました）
http://www.amazon.co.jp/exec/obidos/ASIN/4839952957/hatena-blog-22/

感想

3完。次は4完したい。